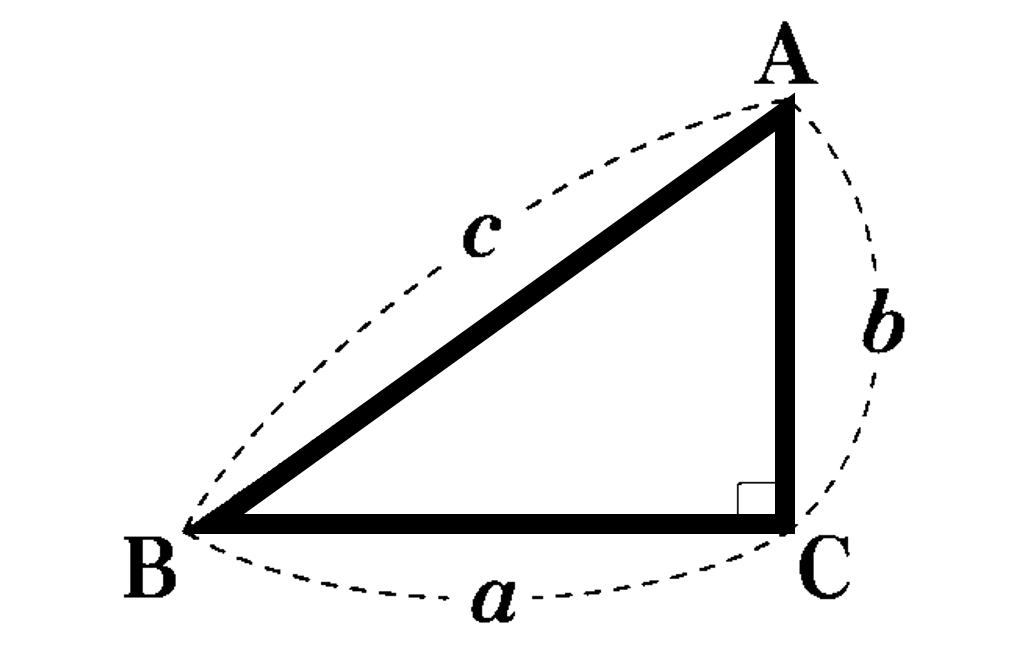
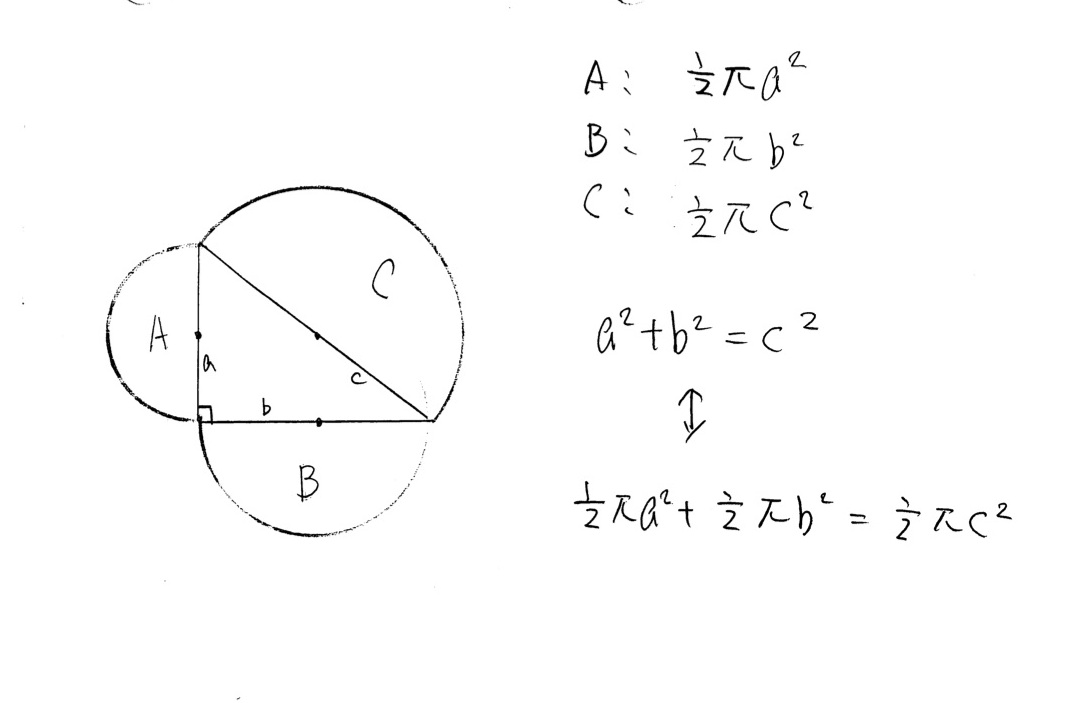
三平方の定理の一般角への応用 三平穂の定理は、あくまでも直角三角形において成り立つ定理ですが、一般角においてはどうなるのでしょうか。それは、高校数学で学ぶ、第二余弦定理というもので、以下のように表されます。 c² = a² b² – 2ab・cosC
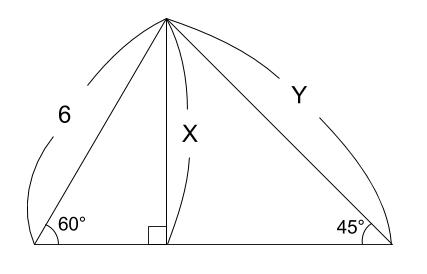
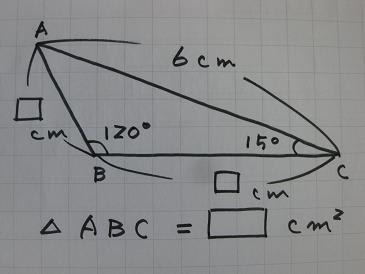
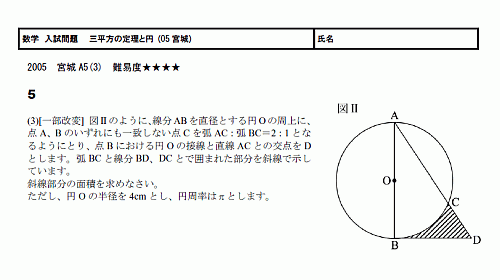
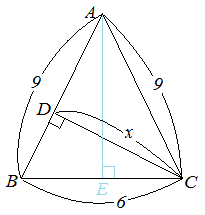
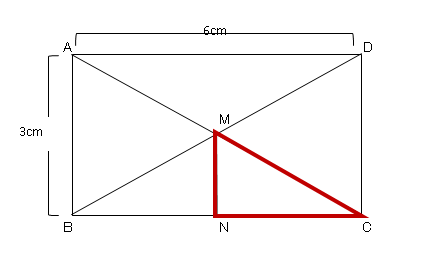
三平方の定理 問題 応用- 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に数学 中学3年生の選択ページに戻る 円と三平方の定理 円と接線の問題で、三平方の定理を用いながら解く問題について学習します。 共通接線;
三平方の定理 問題 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
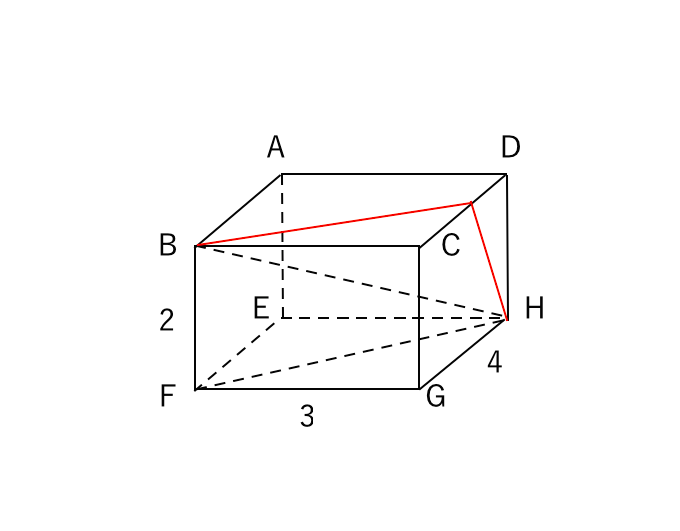 | 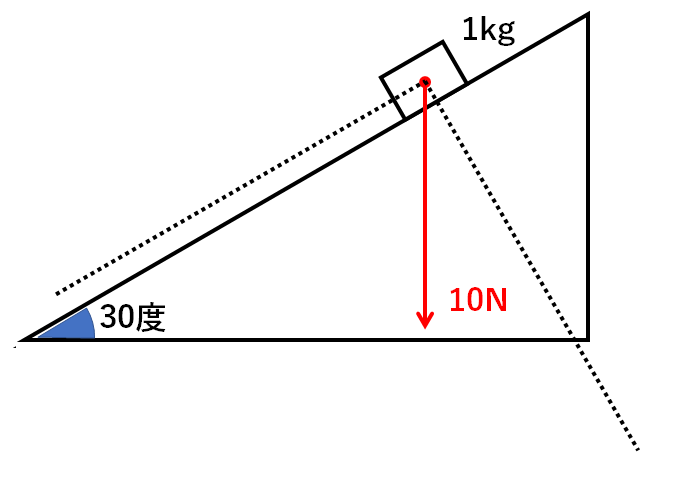 | |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 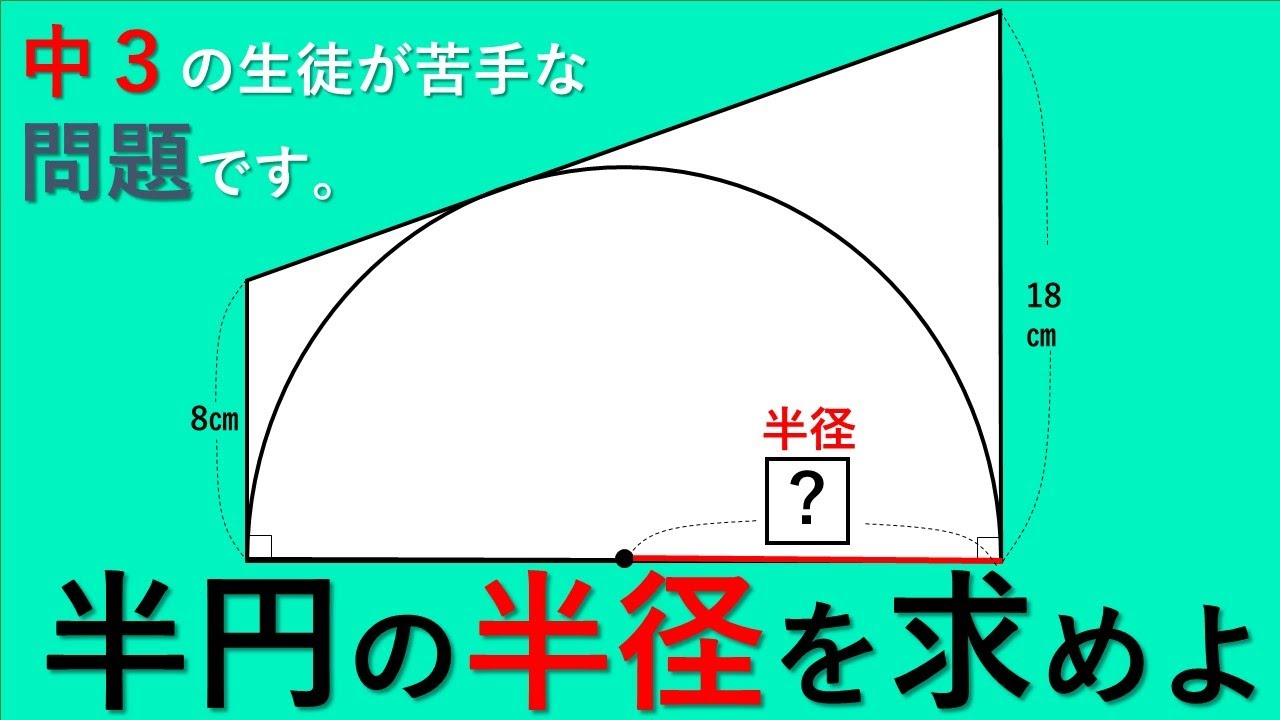 | 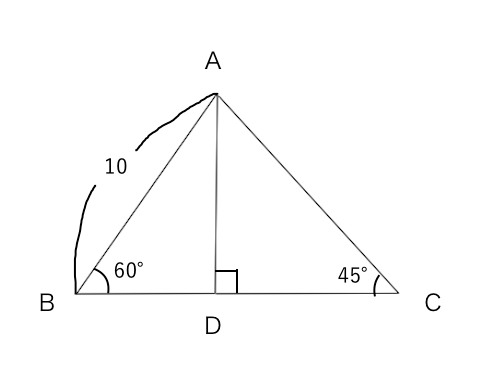 |
 |  |  |
 |  |  |
 |  | |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 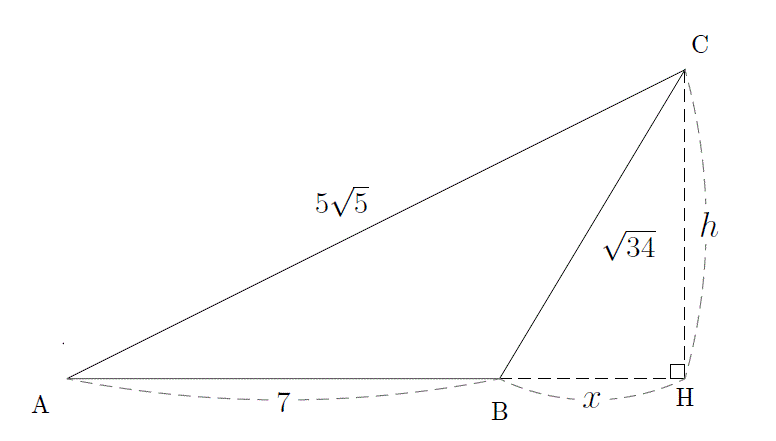 | |
 |  |  |
 | ||
 |  |  |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三平方の定理 問題 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
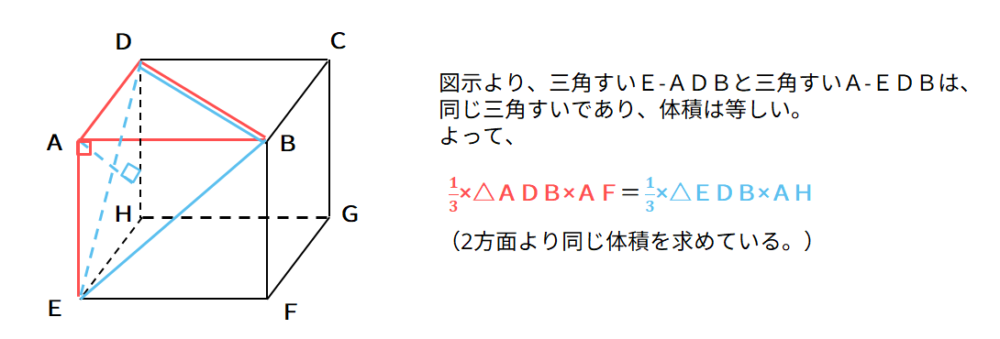
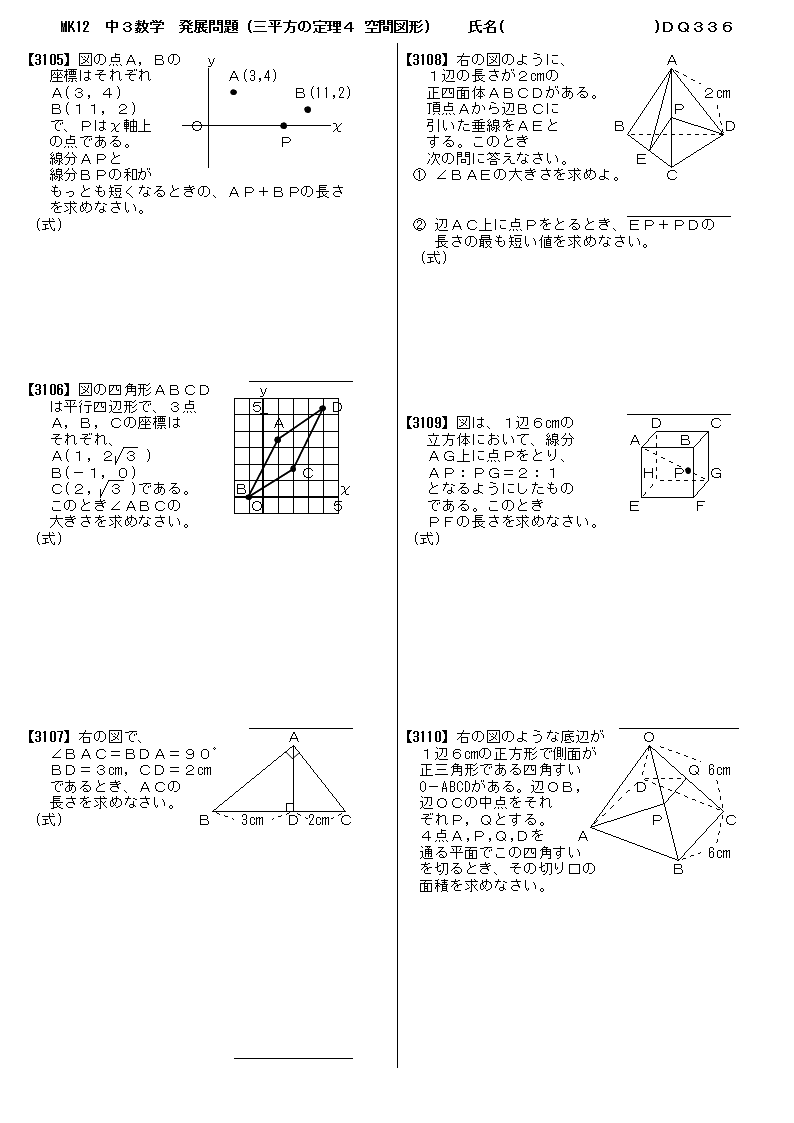
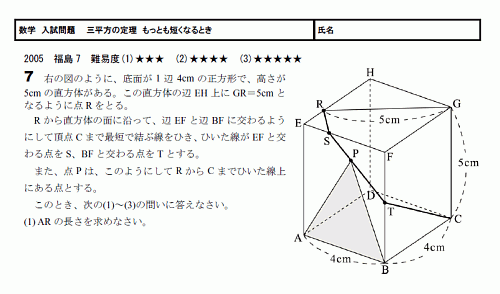
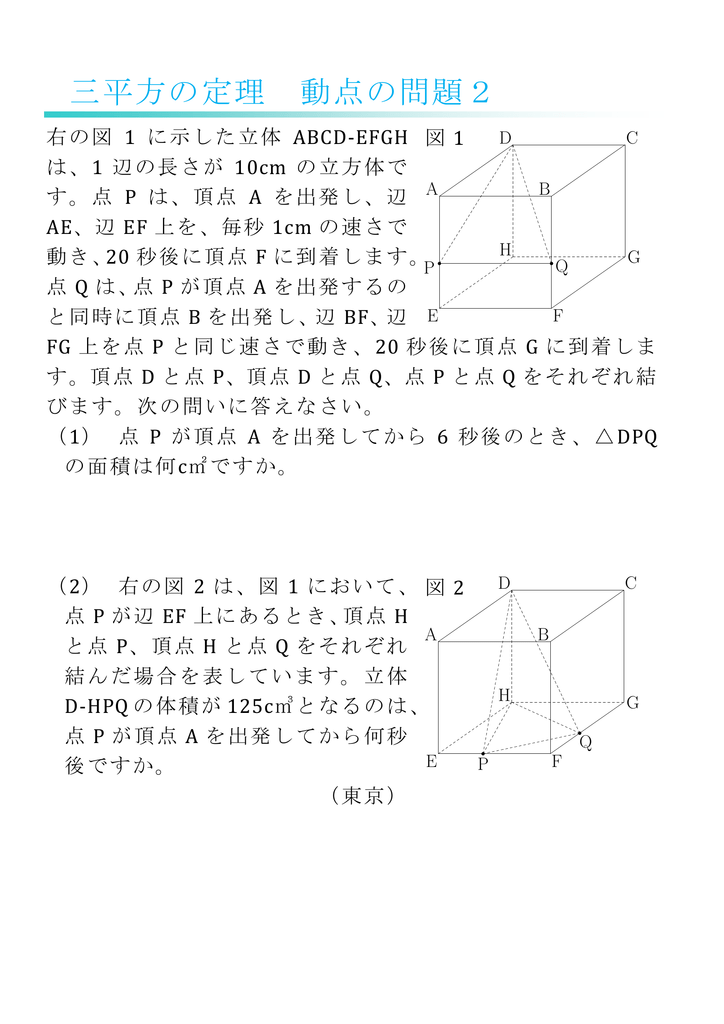
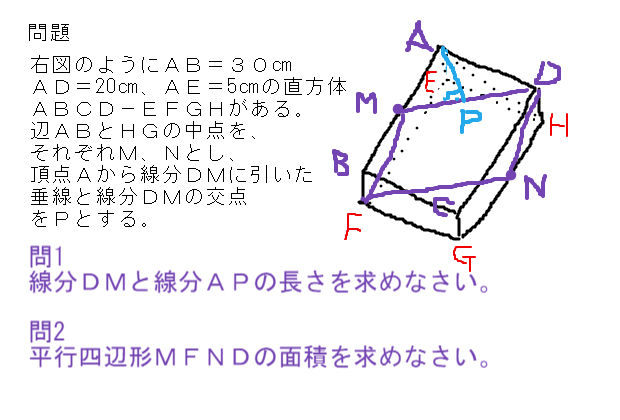
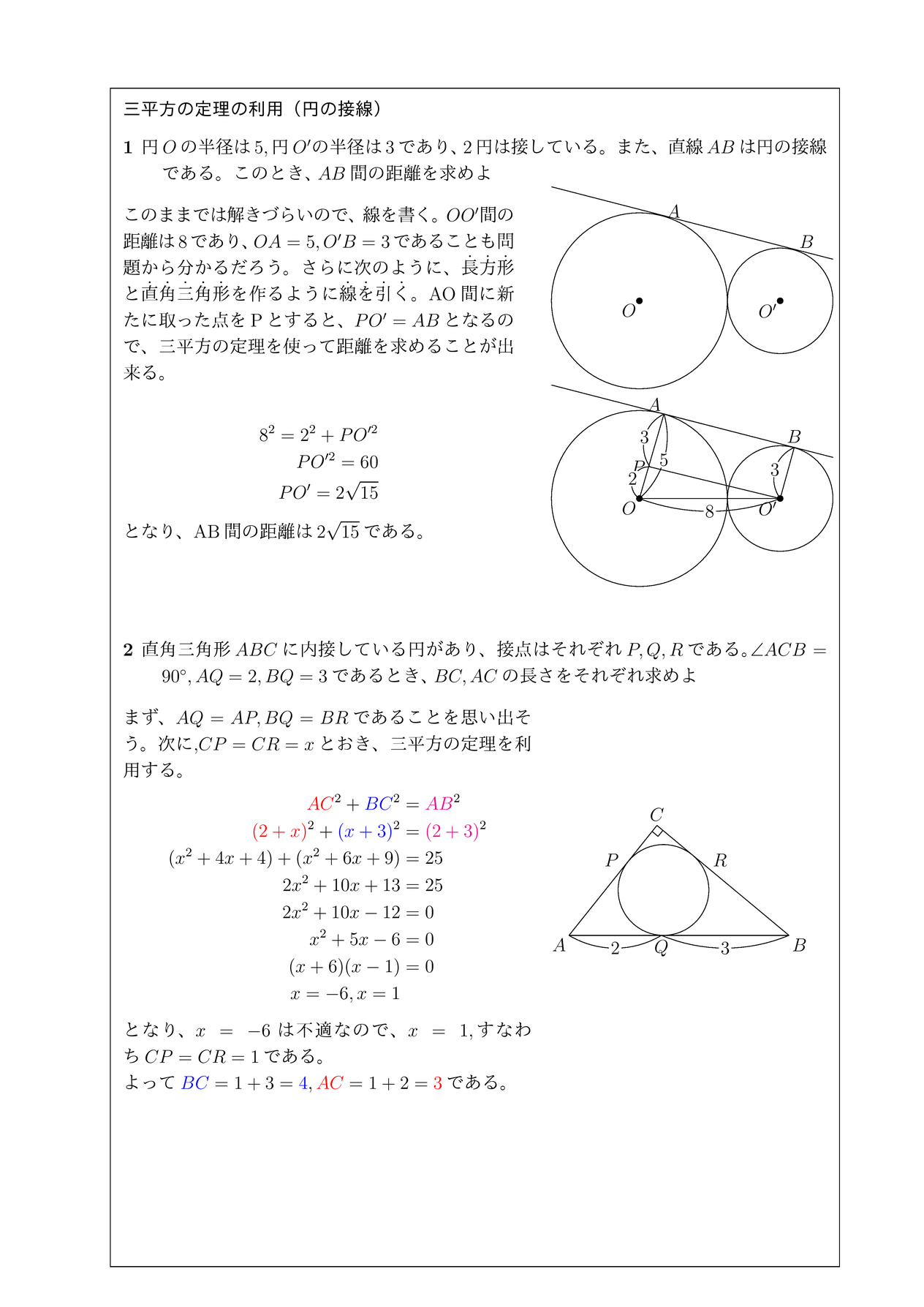
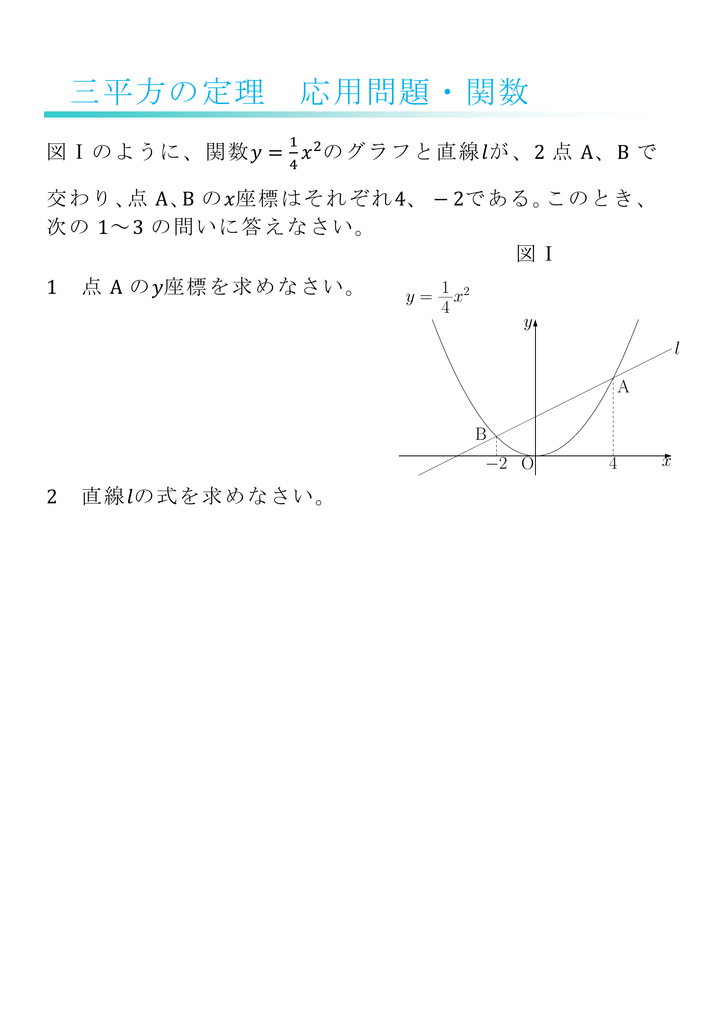
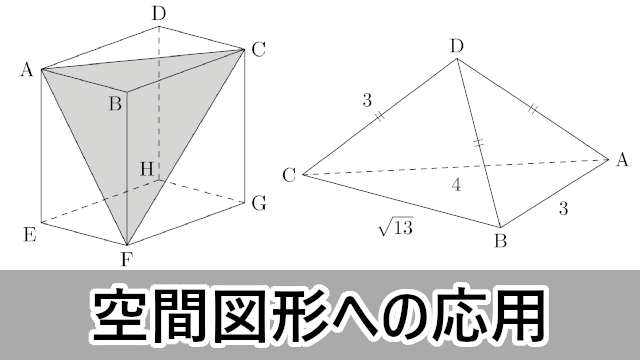
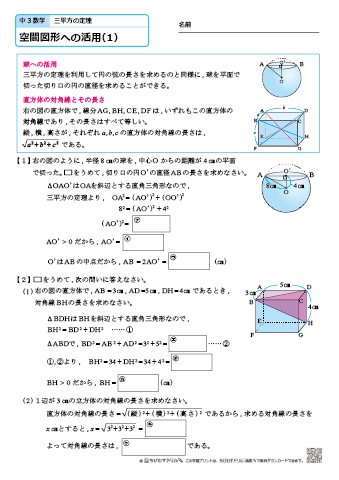
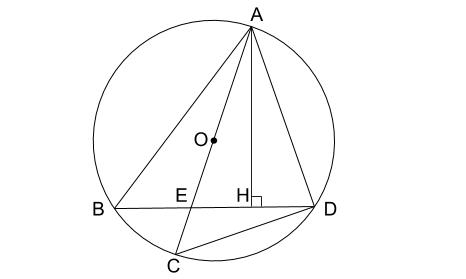
応用問題 直角三角形の中にできる最大の正方形の面積(相似な図形) ヒポクラテスに挑戦(三平方の定理) 最短コースの距離は?(三平方の定理) 切り取った立体について考えよう(空間図形) 円の半径を求めよう(平面図形) 面積の二等分(1)(平面図形) 面積の二等分(2)(平面三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し 共通接線 四角錐の体積 最短の道のり
Incoming Term: 三平方の定理 問題 応用,




0 件のコメント:
コメントを投稿